天津市自考00142计量经济学考试大纲

天津市高等教育自学考试课程考试大纲

课程名称：计量经济学                                            课程代码：00142

第一部分   课程性质与目标

一、课程性质与特点

本课程是高等教育自学考试经济学（专升本）专业的一门专业基础课，它是经济学的一个分支学科，是以揭示经济活动中客观存在的数量关系为内容的分支学科。本课程采用数学和统计学的方法研究经济学问题，在经济理论和经济现象之间搭建了桥梁，在描述经济现实、检验经济理论的假设、预测未来经济活动等方面发挥了重要作用。

二、课程目标与基本要求

设置本课程旨在培养学生科学的思辨能力和认识世界、发现规律的能力。通过本课程的学习，学生可以系统了解计量经济学的基本概念，掌握计量经济学建模的基本思想和原理，熟知计量经济分析的基本方法与步骤，具备运用计量经济模型分析现实经济问题的能力，并为进一步学习更高层次计量经济学课程奠定坚实的基础。

学习本课程要求以习近平新时代中国特色社会主义理论思想指导经济学研究，了解经济运行规律和经济指标的内在联系。熟练掌握计量经济学模型的估计理论和检验方法，了解经济数据的收集方法，掌握计量经济软件的基本操作。引导学生关注社会民生，关切经济现实，熟悉国家经济建设和改革等方面的基本方针政策，围绕实际经济问题开展建模分析。

第二部分   考核内容与考核目标

第一章   绪论

一、学习目的与要求

本章介绍计量经济学的基本概念、经典计量经济学模型的建模步骤和要点，以及计量经济学模型的应用三方面内容。要求通过本章学习，了解计量经济学建立和发展的历史背景与演进历程概貌；明确计量经济学的学科性质和内容体系；对计量经济学模型的建模方法与步骤形成初步认识；对其应用范围有大致了解。

二、考核知识点与考核目标    

（一）计量经济学概述

1.计量经济学的定义（重点）：

识记：计量经济学是经济学的一个分支学科，是以揭示经济活动中客观存在的数量关系为内容的一门经济学方法论学科。其核心是建立计量经济学模型。计量经济学在经济学科中已占据重要地位。

理解：计量经济学的产生与发展。

20世纪20年代末30年代初诞生，1926年挪威经济学家R.Frish提出Econometrics，1930年成立世界计量经济学会，1933年创刊《Econometrica》，20世纪40、50年代的大发展和60年代的扩张，20世纪70年代的批评和反思，20世纪70年代末以来非经典（现代）计量经济学的发展。

2.计量经济学模型（一般）

识记：计量经济模型揭示经济活动中各个因素之间的定量关系，用随机性的数学方程加以描述。

理解：模型、数学模型、经济数学模型、数理经济模型、计量经济学模型（截面数据模型、时间序列数据模型、面板数据模型）

计量经济学模型在经济分析中的地位：

经济理论分析（行为分析）→数理分析 →数量分析（主要是计量经济分析）

3.计量经济学的内容体系（一般）

理解：各种分类：

广义计量经济学和狭义计量经济学；

初、中、高级计量经济学；

理论计量经济学和应用计量经济学；

经典计量经济学和非经典计量经济学；

微观计量经济学和宏观计量经济学。

（二）建立经典单方程计量经济学模型的步骤和要点

1.建立计量经济学模型的步骤（重点）

识记：理论模型的设计（确定模型包含的变量、确定模型的数学形式、拟定理论模型中待估计参数的理论期望值）

样本数据的收集（常用数据类型、样本数据质量）

模型参数的估计

模型的四级检验（经济意义检验、统计检验、计量经济学检验、模型预测检验）

2.计量经济学模型成功的三要素（重点）

识记：经济理论、建模方法、高质量数据

（三）计量经济学的应用（重点）

识记：计量经济学模型的应用主要涉及四个方面：结构分析、经济预测、政策评价、检验与发展经济理论。

理解：结构分析：弹性分析、乘数分析与比较静力分析；

经济预测：短期预测与中长期预测；

政策评价：研究不同的政策对经济运行的影响，并从中选择相对适当的政策的一种模拟性试验，起到“经济政策实验室”的作用；

检验与发展经济理论：通过实际数据考察理论的适用性并发展新的适用的经济学理论。

    第二章   经典单方程计量经济学模型：一元线性回归模型

一、学习目的与要求

本章介绍了回归分析的基本思想与基本方法。要求通过本章学习，了解回归分析的基本概念，掌握计量经济学模型的应用；明确总体回归函数和样本回归函数的区别与联系；对随机干扰项有更为深刻的认识。熟练总体线性回归模型的基本假设；了解最小平方准则及最小平方估计的过程。掌握一元线性回归模型参数估计量的统计性质；了解估计量的概率分布以及随机干扰项方差的估计方法。同时掌握多元线性回归模型的估计和检验方法，深入领会估计系数的解读，包括经济意义和统计意义。

二、考核知识点与考核目标：       

（一）回归分析概述

1.回归分析基本概念（重点）

识记：回归分析(regression analysis)是研究一个变量关于另一个（些）变量的具体依赖关系的计算方法和理论。

理解：相关分析与回归分析的联系与区别。

回归分析构成计量经济学的方法论基础，其主要内容包括：根据样本观察值对计量经济学模型参数进行估计，求得样本回归函数；对样本回归函数、参数估计值进行统计显著性检验；利用样本回归函数进行分析、评价及预测。

2.总体回归函数（一般）

3.随机误差项（次重点）

理解：随机误差项：观察值围绕它的期望值的离差（deviation），是一个不可观测的随机变量，又称为随机误差项（stochastic error）或随机扰动项（stochastic disturbance）。

随机误差项主要包括下列6方面因素：代表未知的因素；代表残缺数据；代表众多细小影响因素；代表数据观测误差；代表模型设定误差；变量的内在随机性。

4.样本回归函数（次重点）

如何获取线性的样本回归函数：采用普通最小二乘法（OLS）

（二）一元线性回归模型的参数估计

1.参数估计的普通最小二乘法（重点）

理解：最小二乘原理。

应用：采用Eviews进行OLS估计。

2.拟合优度（次重点）

理解：总离差平方和的分解、可决系数R²统计量

（三）一元线性回归模型的基本假设与普通最小二乘估计量的统计性质

1.对模型设定的假设（一般）

理解：假设1：回归模型是正确设定的（模型选择了正确的变量；模型选择了正确的函数形式）

2.对解释变量的假设（一般）

理解：假设2：解释变量X在简单随机抽样中具有变异性，而且随着样本容量的无限增加，解释变量X的样本方差依概率收敛于一非零的有限常数。

3.对随机干扰项的假设（重点）

识记：假设3：条件零均值假设。

假设4：同方差性及不序列相关性假设。

假设5：服从零均值、同方差的正态分布假设。

4.普通最小二乘估计量的统计性质（重点）

识记：在基本假设成立的条件下，OLS估计量具有良好的小样本性质：

线性性(linear)，即它是否是另一随机变量的线性函数；

无偏性(unbiased)，即它的均值或期望值是否等于总体的真实值；

有效性(efficient)，即它是否在所有线性无偏估计量中具有最小方差。

这三个准则也称作估计量的小样本性质。拥有这类性质的估计量称为最佳线性无偏估计量（best liner unbiased estimator, BLUE）。

理解：当不满足小样本性质时，需进一步考察估计量的大样本或渐近性质(asymptotic properties)：

渐近无偏性，即样本容量趋于无穷大时，是否它的均值序列趋于总体真值；

一致性，即样本容量趋于无穷大时，它是否依概率收敛于总体的真值；

渐近有效性，即样本容量趋于无穷大时，是否它在所有的一致估计量中具有最小的渐近方差。

（四）一元线性回归模型的统计检验

1.参数估计量的概率分布及随机干扰项方差的估计（次重点）

理解：普通最小二乘估计量的分布形式、总体方差的最小二乘估计量

2.变量的显著性检验（重点）

理解：假设检验。

所谓假设检验，事先对总体参数或总体分布形式作出一个假设，然后利用样本信息来判断原假设是否合理，即判断样本信息与原假设是否有显著差异，从而决定是否接受或否定原假设。假设检验采用的逻辑推理方法是反证法。

应用：t检验。

检验解释变量对被解释变量是否存在着显著的线性影响关系。

3.参数检验的置信区间估计（重点）

理解：通过总体参数的样本估计值寻找参数某一置信度下可能取值的区间范围，它也在一定程度上是对样本回归函数与总体回归函数“接近”程度的检验。

应用：总体参数的置信区间估计

（五）一元线性回归分析的应用：预测问题（一般）

理解：预测值是条件均值或个别值的一个无偏估计

应用：总体条件均值和个别值预测值的置信区间

第三章   经典单方程计量经济学模型：多元线性回归模型

一、学习目的与要求

本章将一元回归模型拓展到了多元回归模型，其基本的建模思想与建模方法与一元情形相同。主要内容包括模型的基本假定、模型的估计、模型的检验以及模型在预测方面的应用等。要求通过本章学习，理解多元线性回归模型的定义，及其与一元线性回归模型的区别和联系；牢记多元线性回归模型的基本假定。同时掌握多元线性回归模型的估计和检验方法，深入领会估计系数的解读，包括经济意义和统计意义。

二、考核知识点与考核目标       

（一）多元线性回归模型

1.多元线性回归模型的形式（次重点）

识记：总体回归函数、总体回归模型、样本回归函数、样本回归模型的矩阵表达式

    2.多元线性回归模型的基本假定（重点）

识记：假设1：回归模型是正确设定的。

假设2：多个解释变量间不存在完全多重共线性。

假设3：随机干扰项具有条件零均值性。

假设4：随机干扰项具有条件同方差性及不序列相关性。

假设5：随机干扰项满足正态分布。

（二）多元线性回归模型的参数估计

1.普通最小二乘估计（重点）：

识记：根据被解释变量的所有观测值与估计值之差的平方和最小的原则求得参数估计量。

理解：普通最小二乘估计及其矩阵表达、随机误差项方差的普通最小二乘估计（无偏估计）

2.拟合优度（一般）

    3.多元线性回归模型估计实例（一般）

应用：采用Eviews进行OLS估计。

（三）多元线性回归模型的统计性质与统计检验

1.参数估计量的统计性质（重点）

识记：小样本性质：线性性、无偏性、有效性

理解：大样本性质：渐近无偏性、渐近有效性、一致性

2.变量的显著性检验（重点）

识记：t检验：

检验解释变量对被解释变量是否存在着显著的线性影响关系。

3.方程的显著性检验（重点）

识记：F检验：

方程的显著性检验，旨在对模型中被解释变量与解释变量之间的线性关系在总体上是否显著成立作出推断。

4.参数的置信区间（次重点）

理解：如何才能缩小置信区间？

增大样本容量n、提高模型的拟合优度、提高样本观测值的分散度。

（四）多元线性回归模型的预测（一般）

应用：E(Y₀)和Y₀的置信区间

（五）含有虚拟变量的多元线性回归模型

1.含有虚拟变量的模型（一般）

一般地，在虚拟变量的设置中：基础类型、肯定类型取值为1；比较类型，否定类型取值为0。

虚拟变量模型：同时含有一般解释变量与虚拟变量的模型称为虚拟变量模型或者方差分析（analysis-of variance: ANOVA）模型。

2.虚拟变量的引入（一般）

加法方式、乘法方式

3.虚拟变量的设置原则（次重点）

每一定性变量(qualitative variable)所需的虚拟变量个数要比该定性变量的状态类别数(categories)少1。即如果有m种状态，只在模型中引入m-1个虚拟变量，避免“虚拟变量陷阱”。

第四章   经典单方程计量经济学模型：放宽基本假定的模型

一、学习目的与要求

本章主要介绍计量经济模型的二级检验问题，即计量经济检验；主要讨论对回归模型若干基本经典假设是否成立进行检验，当检验发现假设不成立时继续采用OLS估计模型所带来的不良后果以及如何修正等问题。具体包括多重共线性问题、异方差性问题、内生解释变量问题。

二、考核知识点与考核目标       

（一）多重共线性

识记：1.多重共线性的含义（重点）：

如果某两个或多个解释变量之间出现了相关性，则称为多重共线性(Multicollinearity)。分为完全共线性与近似共线性两类。

理解：2.实际经济问题中的多重共线性（一般）：

产生多重共线性的主要原因：经济变量相关的共同趋势、模型设定不谨慎、样本资料的限制

识记：3.多重共线性的后果（次重点）：

完全共线性下参数估计量不存在、近似共线性下OLS估计量的方差变大（非有效）、参数估计量经济含义不合理、变量的显著性检验失去意义、模型的预测功能失效

理解：4.多重共线性的检验（一般）：

检验多重共线性是否存在：

对两个解释变量的模型，采用简单相关系数法。

对多个解释变量的模型，采用综合统计检验法。

估计多重共线性的范围，即判断哪些变量之间存在共线性。

判定系数检验法、排除变量法、逐步回归法

应用：5.克服多重共线性的方法（一般）：

第一类方法：排除引起共线性的变量

第二类方法：减小参数估计量的方差

（二）异方差性

识记：1.异方差的类型（重点）：

对于不同的样本点，随机误差项的方差不再是常数，而互不相同，则认为出现了异方差性(Heteroskedasticity)。

异方差一般可归结为三种类型：单调递增型、单调递减型、复杂型。

理解：2.实际经济问题中的异方差性（一般）

识记：3.异方差性的后果（次重点）

参数估计量非有效、变量的显著性检验失去意义、模型的预测失效

理解：4.异方差性的检验（一般）：

      图示检验法、布罗施-帕甘（Breusch-Pagan）检验、怀特（White）检验

应用：5.异方差的修正（一般）

加权最小二乘法（Weighted Least Squares, WLS）、异方差稳健标准误法（Heteroscedasticity-Consistent Variances and Standard Errors）

（三）内生解释变量问题

理解：1.内生解释变量问题的提出（次重点）：

内生随机解释变量与随机干扰项同期相关(contemporaneously correlated)。

理解：2.实际经济问题中的内生解释变量问题主要包括三种情形：（重点）

被解释变量与解释变量具有联立因果关系（simultaneous causality）；模型设定时遗漏了重要的解释变量，而所遗漏的变量与模型中的一个或多个解释变量具有同期相关性（omitting relevant variables）；解释变量存在测量误差（errors-in-variables）。

识记：3.内生解释变量的后果（次重点）

OLS参数估计量是有偏、非一致性估计量。

识记：4.工具变量法（重点）：

    （1）工具变量的选取：

工具变量：在模型估计过程中被作为工具使用，以替代模型中与随机干扰项相关的内生解释变量。

选择为工具变量的变量必须满足以下条件：与所替代的内生解释变量高度相关；与随机干扰项不相关；与模型中其它解释变量不高度相关，以避免出现严重的多重共线性。

（2）工具变量的应用

（3）工具变量法估计量是一致估计量，在小样本下，IV估计量仍是有偏的

（4）两阶段最小二乘法（two stage least squares, 2SLS）。

工具变量法估计过程可等价地分解成两个阶段的OLS回归：

第一阶段，用OLS法进行X关于工具变量Z的回归，并记录X的拟合值；

第二阶段，以得到的X的拟合值代替X 作为解释变量，进行OLS回归。

应用：5.内生性检验与过渡识别约束检验（一般）

          解释变量的内生性建议（Hausman检验）、过度识别约束检验

第五章   时间序列计量经济学模型

一、学习目的与要求

通过本次课的学习，应明确序列相关性的定义；了解序列相关性产生的原因与实际背景；掌握序列相关性存在的后果、序列相关性的检验以及序列相关问题的修正方法。

二、考核知识点与考核目标       

（一）时间序列模型的序列相关性

识记：1.序列相关性（重点）

以截面数据为样本时，如果模型随机项之间存在相关性，称为：Spatial Autocorrelation。以时序数据为样本时，如果模型随机项之间存在相关性，称为：Serial Autocorrelation。习惯上统称为序列相关性（Serial Correlation or Autocorrelation）。

理解：2.实际经济问题中的序列相关性（一般）

经济变量固有的惯性、模型设定偏误、数据的“编造”

识记：3.序列相关性的后果（重点）

参数估计量非有效、变量的显著性检验失去意义、模型的预测失效

理解：4.序列相关性的检验（一般）

      图示法、回归检验法、杜宾-瓦森（Durbin-Watson）检验法、拉格朗日乘数（Lagrange multiplier）检验

应用：5.序列相关的补救（一般）

广义最小二乘法（GLS: Generalized least squares）、广义差分法(Generalized Difference)、稳健标准误法（Newey-West standard errors）

第六章   非经典截面数据计量经济学模型

一、学习目的与要求

通过本次课的学习，明确二元离散选择模型的含义及其应用背景；了解二元离散选择模型的预估计程序；掌握二元离散选择模型的参数估计方法；掌握二元离散选择模型的拟合优度检验、总体显著性检验和预测检验。

二、考核知识点与考核目标       

（一）二元离散选择模型

理解：1.二元离散选择模型的经济背景（一般）

理解：2.二元离散选择模型

      原始模型、效用模型

应用：3.二元离散选择模型的参数估计（次重点）

     极大似然估计、二元Probit离散选择模型及其参数估计、二元离散选择Logit模型及其参数估计

应用：4.Probit模型模拟与预测（一般）

理解：5.二元离散选择模型的检验（一般）

      拟合优度检验（McFadden R²）、总体显著性检验、预测（回代）效果检验

第三部分   有关说明与实施要求

一、考核目标的能力层次表述

    本课程的能力考核目标共分为三个能力层次：“识记”、“理解”、“应用”。各能力层次为递进等级关系，后者必须建立在前者的基础上，其含义是：
    识记：能够识别和记忆本课程中的有关名词、概念及规律的主要内容，并能够根据考核的不同要求，做出正确的表述、选择和判断。

    理解：能够领悟和理解本课程中有关概念及规律的内涵，全面把握基本概念、基本原理、基本方法，能掌握有关概念、原理、方法的区别与联系，并能够根据考核的不同要求，对问题进行逻辑推理和论证，做出正确的判断、解释和说明。

应用（包含简单应用和综合应用）：能在理解掌握的基础上，联系实际、了解计量经济分析方法在经济学科的发展和实际经济工作中的作用，是既要求理论掌握、又要求具备实证分析能力的高层次要求；能熟知计量经济分析的基本方法与步骤，具备运用计量经济模型分析现实经济问题的能力，是最高层次的要求。

二、指定教材

指定教材为考生自学、社会助学和考试命题的依据。

指定教材：《计量经济学》（第五版） 李子奈 潘文卿编著 高等教育出版社 2020年10月

三、自学方法指导

1、自学时必须要认真阅读教材，开始阅读每一章之前，应先认真学习大纲中有关该章的考核知识点、自学要求以及对知识点的能力层次要求和考核要求。以便在阅读教材时做到心中有数，有的放矢。

2、使用教材时，应注意将精读与泛读相结合，应在泛读即通读的基础和掌握较全面的知识背景条件下，对考核知识点进行重点地逐段细读，逐句推敲，以求做到对基本概念深刻理解，对历史脉络彻底弄清，对基本理论牢固掌握。切忌在没有全面学习教材的情况下孤立地抓考核知识点，以免生吞活剥，不能真正地理解和灵活地运用。

3、在自学过程中，既要思考问题，也要做好阅读笔记，把教材中的基本概念术语、基本理论方法加以整理，归纳出要点，从而加深对问题的认知、理解和记忆。有利于突出重点，并涵盖全部课程内容，同时锻炼提高自己的自学能力。

4、在自学过程中，既要注重理论知识，也应重视实际运用能力的培养。如利用计量经济模型对实际经济问题进行建模分析的方法，包括进行经济结构分析、经济预测、政策评价、检验经济学理论等等。要通过完成练习思考题、撰写小论文，锻炼自己分析论证及书面表达的能力。

5、考生在自学过程中也可参考潘文卿、李子奈主编《计量经济学（第五版）学习指南与练习》（高等教育出版社，2021年版）辅助学习、理解相关知识。

四、对社会助学的要求

1.社会助学者应根据本大纲规定的考试内容和考核目标，认真钻研自学考试指定教材，明确本课程与其他课程不同的特点和学习要求，对自学应考者进行切实有效的辅导，引导他们防止自学中的各种偏向，把握社会助学的正确导向。

2.要正确处理基础知识和应用能力的关系，努力引导自学应考者将识记、理解与应用联系起来，把基础知识和理论转化为应用能力，在全面辅导的基础上，着重培养和提高自学应考者的分析问题和解决问题的能力。

3.要正确处理重点、次重点和一般的关系。课程内容有重点、次重点和一般之分，但考试内容是全面的，而且三者之间是相互联系的，不是截然分开的。社会助学者应指导自学应考者全面系统地学习教材，掌握全部考试内容和考核知识点，在此基础上再突出重点。总之，要把重点学习同兼顾一般结合起来，切勿孤立地抓重点，把自学应考者引向猜题押题。

4．助学学时建议。本课程共6学分，助学建议不少于108学时，课程学时分配见下表，考生也可参考该表安排自学时间。

五、关于命题考试的若干规定

1、本大纲各章所提到的内容和考核目标都是考试的内容。

2、试卷中对不同能力层次要求和试题所占的比例大致是：“识记”为30%，“理解”为40%，“应用”为30%。

3、试题难易程度要合理，可分为四档：易、较易、较难、难，这四档在每份试卷中所占比例依次约为2：3：3：2。

4、每份试卷中，各类考核点所占比例约为：重点占65%，次重点占25%，一般占10%。

5、试题题型一般分为：填空题、选择题（包括单项与多项）、解释概念题、简答题、论述题和分析题等。

6、考试采用闭卷笔试，考试时需携带没有任何存储功能的普通计算器。考试时间为150分钟，采用百分制评分，60分为及格。

六、 题型示例（样题）

（一）填空题

计量经济学是以揭示经济活动中客观存在的数量关系为内容的经济学分支学科，是经济理论、            、数学三者的结合。

（二）单项选择题

    如果线性回归模型中的随机误差项存在异方差，则模型参数的普通最小二乘估计量（    ）。

A.无偏且有效                       B.无偏但非有效

C.有偏但有效                       D.有偏且非有效

（三）多项选择题

经济计量模型的应用方向是（      ）。

A.用于经济预测              B.用于经济政策评价           C.用于结构分析

D.用于检验和发展经济理论    E.仅用于经济预测、经济结构分析

（四）解释概念

1.总体回归函数

2.最小二乘（平方）法

（五）简答题

请简述利用截面数据建立多元线性回归模型所需的假设条件，及其OLS估计量的性质。

（六）论述题

试论述回归分析与相关分析的区别与联系？

（七）分析题

假定要研究成为烟民的概率是否与受教育程度有关，建立如下Probit模型：

其中，被解释变量smoke为虚拟变量，smoke=1表示是烟民；smoke=0表示不是烟民；

核心解释变量educ为教育年限，单位：年；

控制变量包括：income为收入，单位：元；age为年龄，单位：年；

Stata软件的估计结果如下：

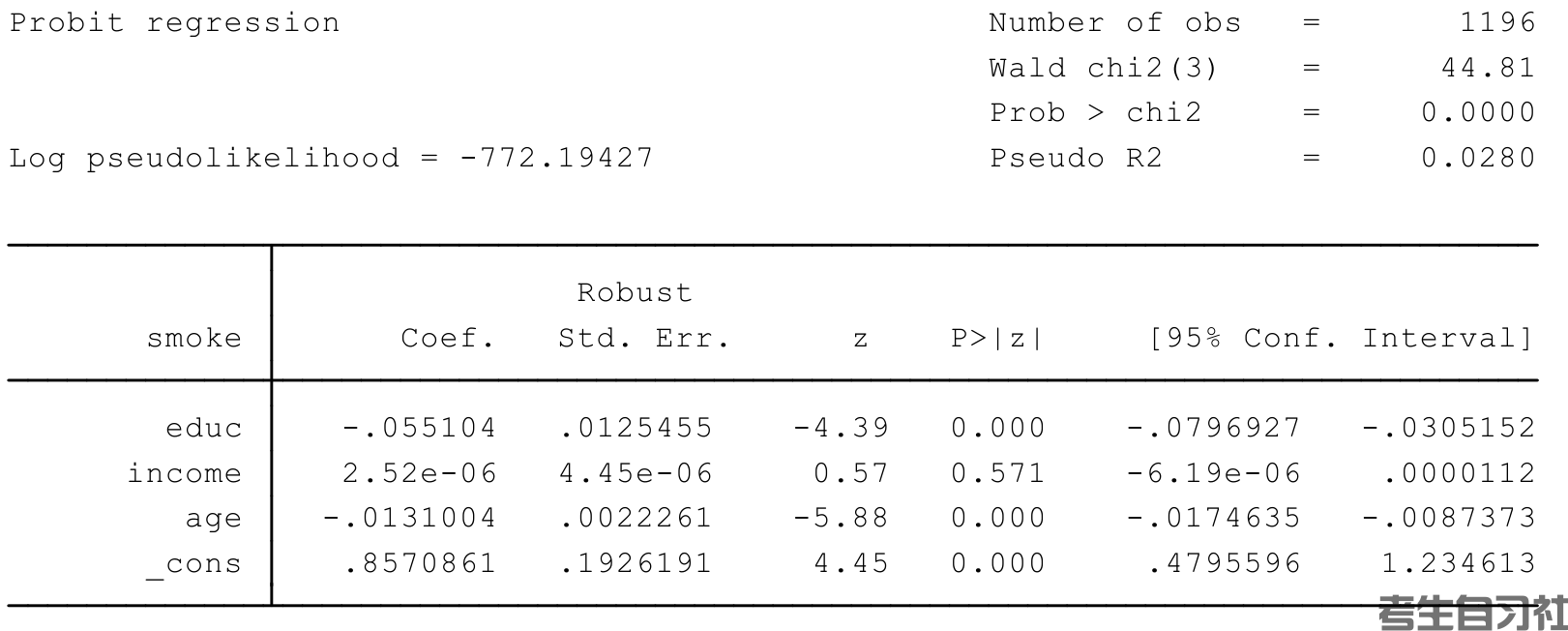
根据如上说明回答以下问题：

1.写出样本回归线、稳健标准误和概括统计量。

2.在0.05的显著性水平下，判断受教育程度educ对是否是烟民的概率的影响是否显著。

3.若某人educ=15，income=12500，age=28，预测其是烟民的概率。